Last updated: December 2025
Background and Basic Idea
Pragmatic cluster randomized trials (CRTs) are increasingly conducted in healthcare delivery systems where patients are nested within providers or clinics. While the average treatment effect (ATE) has been the cornerstone in comparative effectiveness research, there is growing interest in understanding whether the treatment effect varies among pre-specified patient subgroups, addressing the goal of “what works best, and for whom.” This PCORI-funded methodological project (2021-2025, PCORI project page here) aims to develop new sample size formulas and methods for assessing confirmatory heterogeneity of treatment effect (HTE) in various types of CRT designs. The development is largely based on a covariate-by-treatment interaction test derived from random-effects regression models and properly accounts for the multilevel and longitudinal correlation structures of both the outcome and the baseline effect modifiers. The central finding is that the power of the HTE interaction test and hence sample size depend on two types of intraclass correlation coefficients (ICCs):
- Outcome ICC (o-ICC): the correlation between outcomes collected from individuals within the same cluster; this is the typical ICC in the classical CRT literature;
- Covariate ICC (c-ICC): the correlation between effect modifiers (e.g., baseline characteristics) collected from individuals within the same cluster; this is the less familiar ICC that should be considered for determining the power of the interaction test.
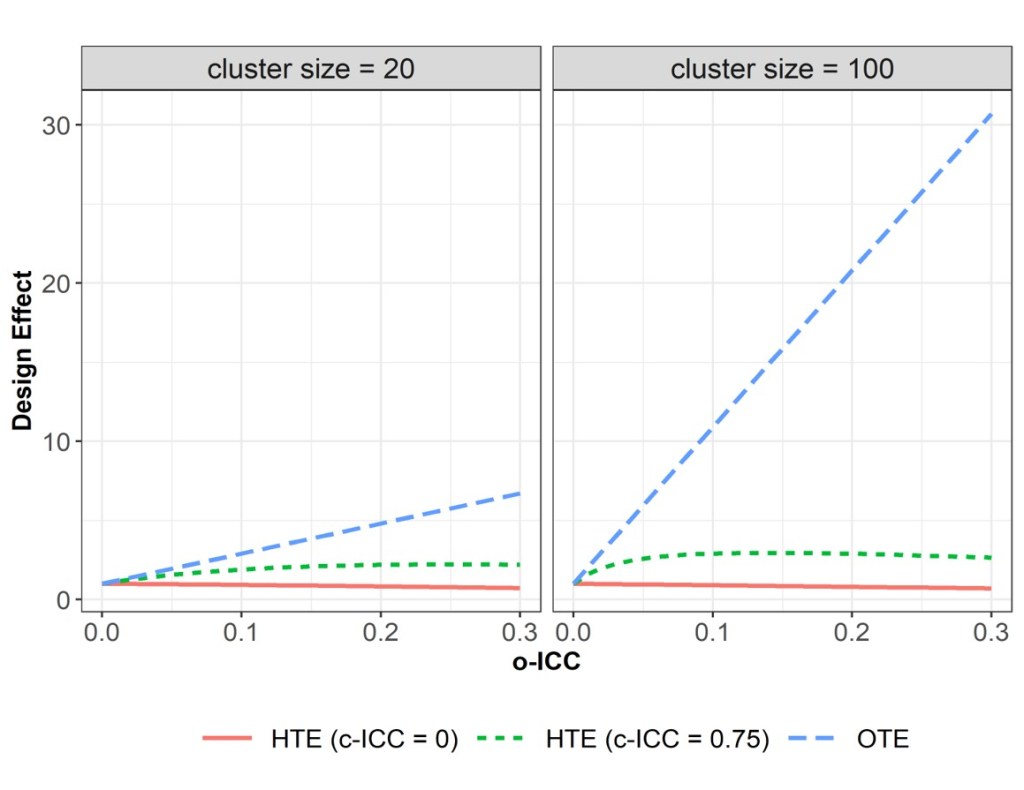
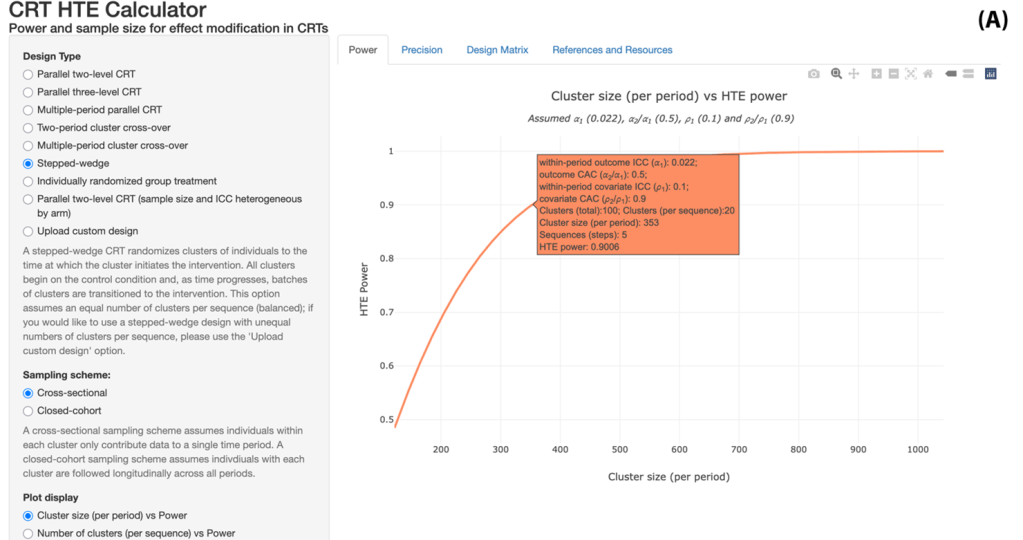
The procedure involves the following steps: (1) Specify design parameters, including number of clusters, cluster size, o-ICC, c-ICC, and the target HTE effect size; (2) Use the developed analytical formulas (or software) to calculate the required sample size or power; (3) Conduct sensitivity analyses by varying ICC parameters over plausible ranges. To support implementation, an R Shiny App (CRT HTE Calculator) and an R package (CRThtePower) have been developed by our team to support this procedure. At this stage, the R Shiny App is more comprehensive and covers almost all types of CRT designs, but only considers a single binary or continuous effect modifier (arguably the most common case). The R package provides functions to support calculations with multivariate effect modifiers, but is currently refined to three-level parallel-arm designs and stepped wedge designs. The companion tutorial article for the R Shiny App can be accessed here and is under revision at International Journal of Epidemiology.
Publication Deliverables
We have developed a collection of new sample size formulas and methods under the simplest parallel-arm cluster randomized trial design, addressing different aspects of complications encountered in statistical practice. These publications include:
- Prototypical development demystifying the role of o-ICC and c-ICC: Yang S, Li F, Starks MA, Hernandez AF, Mentz RJ, Choudhury KR. Sample size requirements for detecting treatment effect heterogeneity in cluster randomized trials. Statistics in Medicine. 2020; 39(28):4218-37.
- Variable cluster sizes may have minimum impact on the interaction test: Tong G, Esserman D, Li F. Accounting for unequal cluster sizes in designing cluster randomized trials to detect treatment effect heterogeneity. Statistics in Medicine. 2022; 41(8):1376-96.
- Generalization to three-level designs with multiple layers of clustering: Li F, Chen X, Tian Z, Esserman D, Heagerty PJ, Wang R. Designing three-level cluster randomized trials to assess treatment effect heterogeneity. Biostatistics. 2023; 24(4):833-49.
- Sample size methods when binary or count outcomes are modeled: Maleyeff L, Wang R, Haneuse S, Li F. Sample size requirements for testing treatment effect heterogeneity in cluster randomized trials with binary outcomes. Statistics in Medicine. 2023; 42(27):5054-83. [R Shiny App for sample size with binary outcomes]
- Sample size methods accounting for missing outcomes: Tong J, Li F, Harhay MO, Tong G. Accounting for expected attrition in the planning of cluster randomized trials for assessing treatment effect heterogeneity. BMC Medical Research Methodology. 2023; 23(1):85.
- Optimal sample size when there is uncertainty in o-ICC and c-ICC: Ryan MM, Esserman D, Li F. Maximin optimal cluster randomized designs for assessing treatment effect heterogeneity. Statistics in Medicine. 2023; 42(21):3764-85. [R Shiny App for local optimal design and maximin design]
- A companion question: how to determine sample size for subgroup effects: Sample size Wang X, Goldfeld KS, Taljaard M, Li F. Sample size requirements to test subgroup-specific treatment effects in cluster-randomized trials. Prevention Science. 2024; (Suppl 3):356-70.
Given many modern healthcare system trials extend beyond the simple parallel-arm CRT design, our team has also provided a set of recent generalizations to address the power of an interaction test in individually-randomized group treatment trials (IRGTs), cluster randomized crossover trials (CRXO Trials), and stepped wedge cluster randomized trials (SW-CRTs). These publications include:
- IRGTs where o-ICC can differ by arm but c-ICC does not vary by arm: Tong G, Taljaard M, Li F. Sample size considerations for assessing treatment effect heterogeneity in randomized trials with heterogeneous intracluster correlations and variances. Statistics in Medicine. 2023; 42(19):3392-412.
- CRXO trials with 2 periods and 2 sequences: Wang X, Chen X, Goldfeld KS, Taljaard M, Li F. Sample size and power calculation for testing treatment effect heterogeneity in cluster randomized crossover designs. Statistical Methods in Medical Research. 2024; 33(7):1115-36.
- SW-CRTs including both cross-sectional and closed-cohort designs: Li F, Chen X, Tian Z, Wang R, Heagerty PJ. Planning stepped wedge cluster randomized trials to detect treatment effect heterogeneity. Statistics in Medicine. 2024; 43(5):890-911.
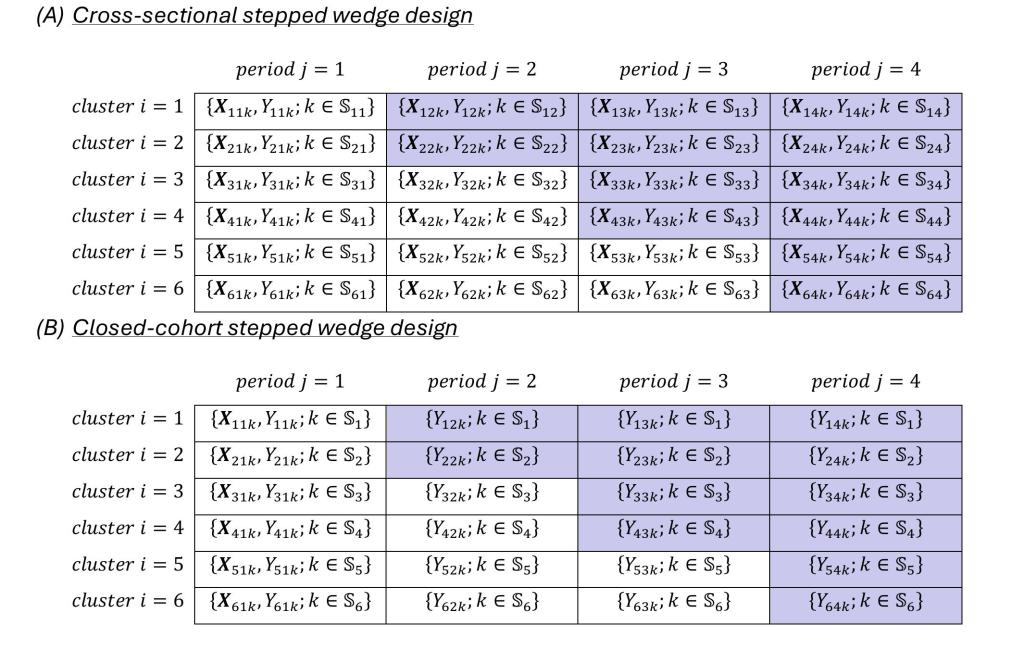
In companion, this project supported several translational tutorial and empirical publications to assist application of the proposed new methods:
- A one-stop shop tutorial for using the CRT HTE Calculator for sample size of an interaction test in various CRTs: Baumann MR, Taljaard M, Heagerty PJ, Harhay MO, Tong G, Wang R, Li F. A tutorial on conducting sample size and power calculations for detecting treatment effect heterogeneity in cluster randomized trials. arXiv preprint arXiv:2501.18383. 2025 Jan 30. [R Shiny App CRT HTE Calculator]
- A principled guide to estimate ICC in complex CRT designs: Ouyang Y, Hemming K, Li F, Taljaard M. Estimating intra-cluster correlation coefficients for planning longitudinal cluster randomized trials: a tutorial. International Journal of Epidemiology. 2023; 52(5):1634-47. [R Shiny App for estimating o-ICCs in longitudinal CRTs]
- A first effort to report both o-ICC and c-ICC estimates with empirical data: Ouyang Y, Li F, Li X, Bynum J, Mor V, Taljaard M. Estimates of intra-cluster correlation coefficients from 2018 USA Medicare data to inform the design of cluster randomized trials in Alzheimer’s and related dementias. Trials. 2024; 25(1):732. [Interactive R Shiny App for visualizing empirical o-ICC and c-ICC estimates in the 2018 USA Medicare data base]
Finally, this project also cultivates new methods for estimation; beyond design and sample size considerations, we have contributed approaches for both confirmatory and exploratory HTE analysis in CRTs. The study team is continuing to explore this frontier, and two example methodological developments in this area are:
- What is the best approach for handling missing baseline effect modifiers in CRTs: Blette BS, Halpern SD, Li F, Harhay MO. Assessing treatment effect heterogeneity in the presence of missing effect modifier data in cluster-randomized trials. Statistical Methods in Medical Research. 2024; 33(5):909-27.
- How to leverage machine learning methods to test for the existence of any HTE in CRTs: Maleyeff L, Li F, Haneuse S, Wang R. Permutation tests for detecting treatment effect heterogeneity in cluster randomized trials. Statistical Methods in Medical Research. 2025:09622802251348999.
Primary Investigator Team
- Principal Investigator: Fan Li, PhD, Associate Professor, Department of Biostatistics, Yale School of Public Health
- Co-Investigator: Patrick Heagerty, PhD, Professor, Department of Biostatistics, University of Washington
- Co-Investigator: Rui Wang, PhD, Lagakos and Zelen endowed Chair and Professor, Harvard Pilgrim Health Care Institute and Harvard Medical School
- Co-Investigator: Denise Esserman, PhD, Professor, Department of Biostatistics, Yale School of Public Health
- Co-Investigator: Mary Ryan Baumann, PhD, Assistant Professor, Departments of Population Health Sciences and Biostatistics & Medical Informatics, University of Wisconsin – Madison
Disclaimer and Acknowledgement
This project was supported by the a competitive Patient-Centered Outcomes Research Institute (PCORI) Award ME-2020C3-21072 (total cost $1,069,312, approved in July 2021). The official PCORI webpage can be found here, where one can also locate the peer-reviewed version of the Final Research Report (expected to be online in 2026). All members of the study team expressed sincere gratitude to PCORI for supporting this project and making it possible, thereby enabling the development of this new strand of methodological research. To our knowledge, this work represents the frontier of efforts to advance HTE design and estimation and the broader study of heterogeneous effects in cluster-randomized trials.
The Investigator Team would also like to express their deep gratitude to all collaborators and stakeholder partners who have contributed their expertise and dedication throughout this award. It has been a genuine privilege to work with such an engaged and interdisciplinary team. The stakeholder discussions, in particular, have profoundly shaped the direction of this research and have motivated ideas that extended well beyond the initial proposal. Their insights have enriched the project in ways we did not anticipate and have directly contributed to the fact that we now have far more results and progress than originally envisioned. We are truly thankful for their partnership.
Disclaimer: The statements in this website are solely the responsibility of the authors and study team and do not necessarily represent the views of PCORI, its Board of Governors, or Methodology Committee. The principal investigator Fan Li extends special thanks to Yukang Zeng and Hao Wang for their valuable assistance in developing the initial version of this webpage.