Research

1. Model-Based Methods for Cluster Randomized Trials

Cluster randomized trials (CRTs) are studies in which groups—rather than individuals—are randomized to conditions. Clusters may represent hospitals, clinics, and nursing homes, making CRTs indispensable for evaluating interventions delivered at the system, provider, or community level. As healthcare systems increasingly implement complex, multi-component, and policy-driven interventions, CRTs have become central to pragmatic and implementation research. At the same time, they also raise foundational methodological challenges not encountered in individually randomized trials. Addressing such issues is essential for generating credible, interpretable, and decision-relevant evidence in modern clinical and public health research.

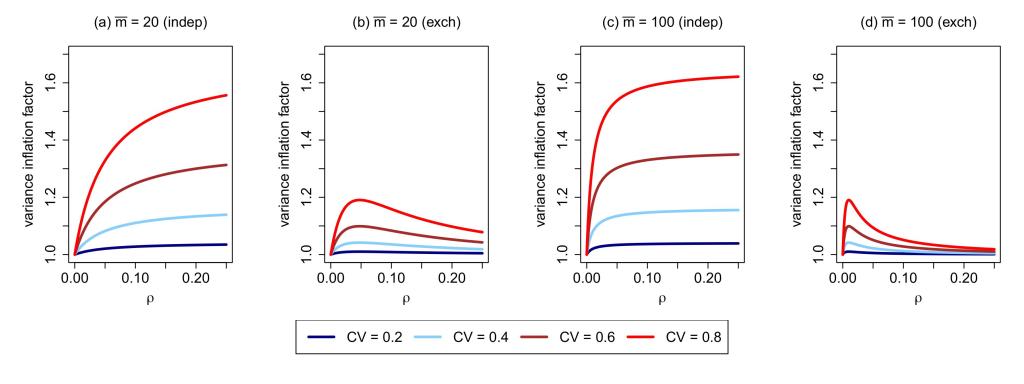
The research in my group advances the methodological foundations for designing and analyzing nearly all major classes of cluster randomized trials (CRTs), including parallel‐arm, crossover, and stepped‐wedge designs. This body of work has directly informed national initiatives such as the NIH Pragmatic Trials Collaboratory and the NIA IMPACT Collaboratory, where our methods guide best practices for planning and conducting pragmatic trials. A central methodological challenge in CRTs is appropriately accounting for the correlated outcomes induced by cluster-level randomization to achieve valid, efficient, and interpretable inference. Key areas of my past and ongoing research that adopt a model-based perspective to address clustering include:

Figure 1. Variance inflation factor due to randomly unequal cluster sizes in parallel-arm CRTs, when comparing (model-based) independence GEE (a,c) and exchangeable GEE (b,d) treatment effect estimators; ρ\rho is the intracluster correlation coefficient (ICC) and m‾\bar{m} is the average cluster size. Hence, formally accounting for clustering through estimating the ICC protects efficiency loss due to random unequal cluster sizes. See Li and Tong (2021) for details.

2. Estimand-Aligned Methods for Cluster Randomized Trials

Beyond specifying statistical models, modern analysis of CRTs increasingly demands clarity about “what treatment effect is being estimated“. In CRTs, the presence of unequal cluster sizes, variable treatment exposure, and post-treatment randomization means that model-based analyses may target different causal quantities depending on the choice of working model and scale. This has elevated the role of estimands—well-defined, model-free descriptions of the causal effect of interest—as a cornerstone of contemporary cluster trial interpretation. Estimands are now recognized internationally, including through ICH E9(R1) Addemdum, as essential for ensuring that what is estimated aligns with the scientific question and supports transparent, policy-relevant decision-making.

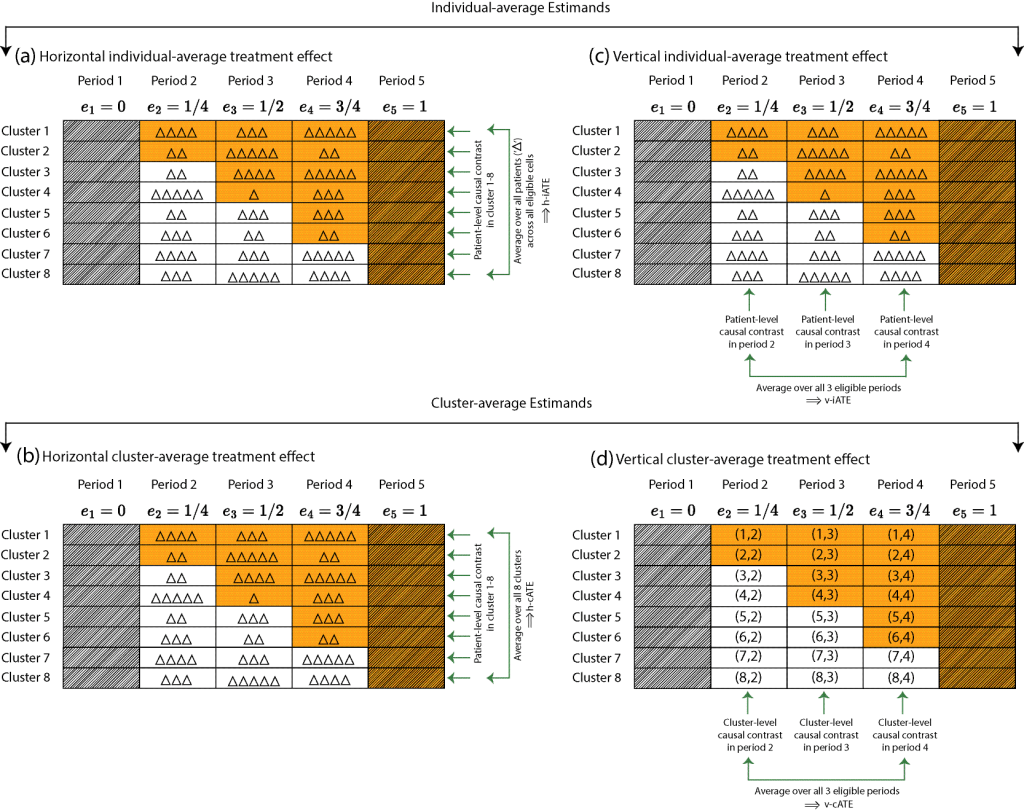
Figure 2. A schematic illustration of different treatment effect definitions in a hypothetical cross-sectional SW-CRT with 8 clusters and 5 periods. The hatch-mark shaded cells in periods 1 and 5 correspond to periods where the propensity score is 0 or 1, hence the unobserved potential outcomes are not identifiable under our nonparametric causal model framework. White (non-shaded) cells in periods 2–4 indicate control cluster-periods and colored cells in periods 2–4 indicate intervention cluster-periods that are eligible in a sense that the propensity score is neither 0 nor 1 (hence satisfying the overlap assumption). See Fang et al. (2025) for full details.

The research in my group contributes to the evolving literature on estimand-aligned frameworks for CRTs that separate the scientific target from the statistical model, clarifying the distinction between cluster-average and individual-average treatment effects and enabling valid inference even under baseline adjustment, informative cluster size and post-randomization bias. Several interest areas include:

3. Causal Inference for Addressing Confounding, Moderation and Mediation

Causal inference from observational data is essential for understanding how interventions perform in real-world settings, where treatment assignment is non-random and multiple biases arise. My work develops statistically rigorous methods that enable credible effect estimation in the presence of confounding, measurement error, limited overlap, and complex longitudinal treatment structures. I am interested in advancing estimators grounded in semiparametric efficiency theory, and debiased machine learning to obtain robust average and heterogeneous treatment effects. I also advance causal mediation methods to uncover mechanisms, and develop machine-learning–integrated strategies for effect moderation with valid uncertainty quantification. Some of my example works include:

Figure 3. Causal diagrams in a hypothetical cluster randomized trial with an individual-level mediator; full descriptions can be found in Cheng and Li (2024)

4. Addressing Intercurrent Events under Estimands Framework

Modern clinical research increasingly requires clarity about how treatment effects are defined when intercurrent events, such as death, treatment switching, or non-adherence, interrupt or modify the interpretation of outcomes. The ICH E9(R1) Addendum Estimands Framework has fundamentally reshaped this landscape by emphasizing that analyses must target well-defined estimands that transparently link the scientific question to the treatment effect being estimated. This guidance has made explicit that treatment effects can differ drastically depending on how intercurrent events are handled, and that ambiguity in these choices undermines interpretability, comparability, and regulatory decision-making. A translational article on this point can be found here:

Table 1. Different strategies for handling intercurrent events; a more complete table can be found in Kahan et al. (2023).

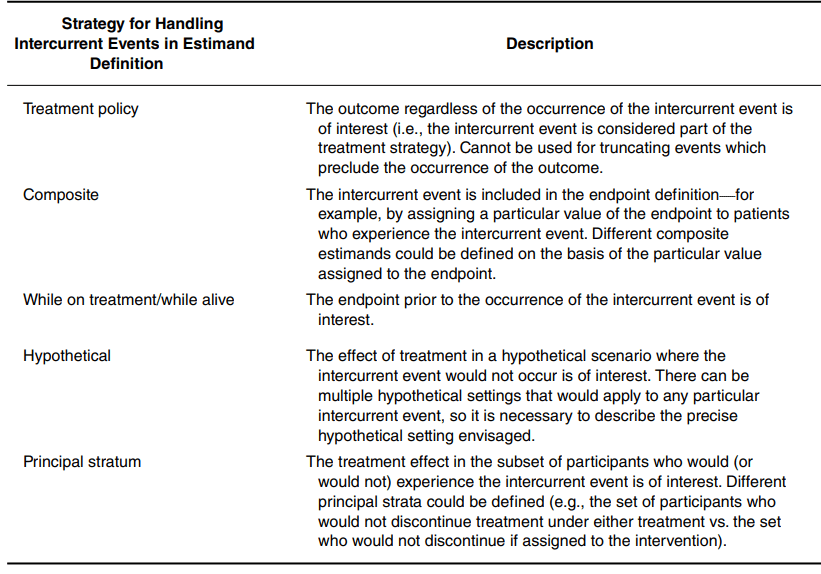
My group advances practice with the Estimands Framework by focusing on three strategies for handling intercurrent events that remain less familiar yet offer substantial room for methodological innovation:

Beyond statistical methodology research, I have a broad interest in translational and collaborative research, including but not limited to cardiology, critical care, geriatrics, nephrology, and implementation science.